

In the sodium chloride case, that would be +787 kJ mol -1.īoth refer to the same enthalpy diagram, but one looks at it from the point of view of making the lattice, and the other from the point of view of breaking it up. In other words, you are looking at an upward arrow on the diagram. Or, you could describe it as the enthalpy change when 1 mole of sodium chloride (or whatever) is broken up to form its scattered gaseous ions.In the sodium chloride case, that would be -787 kJ mol -1. In other words, you are looking at a downward arrow on the diagram. You could describe it as the enthalpy change when 1 mole of sodium chloride (or whatever) was formed from its scattered gaseous ions.So lattice enthalpy could be described in either of two ways.

Remember that energy (in this case heat energy) is given out when bonds are made, and is needed to break bonds. You can show this on a simple enthalpy diagram.įor sodium chloride, the solid is more stable than the gaseous ions by 787 kJ mol -1, and that is a measure of the strength of the attractions between the ions in the solid. Those forces are only completely broken when the ions are present as gaseous ions, scattered so far apart that there is negligible attraction between them. The greater the lattice enthalpy, the stronger the forces. Lattice enthalpy is a measure of the strength of the forces between the ions in an ionic solid.
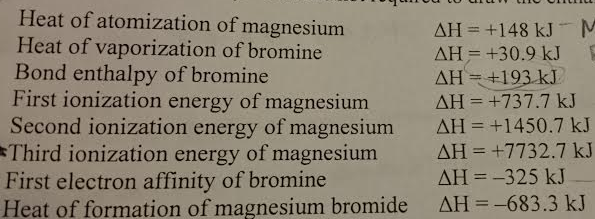
I will explain how you can do this in a moment, but first let's look at how the problem arises. In fact, there is a simple way of sorting this out, but many sources don't use it. There are two different ways of defining lattice enthalpy which directly contradict each other, and you will find both in common use. Two different ways of defining lattice enthalpy Just don't assume that any bit of data you are given (even by me) is necessarily "right"! It doesn't affect the principles in any way. Values from this now fairly old book often differ slightly from more recent sources.ĭon't worry about this. These came from the Chemistry Data Book edited by Stark and Wallace, published by John Murray. If you use my chemistry calculations book, you will find a slightly different set of numbers. If you are doing a course for 16 - 18 year olds, none of this really matters - you just use the numbers you are given. In the Born-Haber cycles below, I have used numbers which give a consistent answer, but please don't assume that they are necessarily the most accurate ones. Note: While I have been writing this section, the different values for the same piece of data from different data sources has driven me crazy, because there is no easy way of knowing which is the most recent or most accurate data.
Unless you go on to do chemistry at degree level, the difference between the two terms isn't likely to worry you. However, the difference is small, and negligible compared with the differing values for lattice enthalpy that you will find from different data sources. In fact, there is a difference between them which relates to the conditions under which they are calculated. Lattice enthalpy and lattice energy are commonly used as if they mean exactly the same thing - you will often find both terms used within the same textbook article or web site, including on university sites. This page introduces lattice enthalpies (lattice energies) and Born-Haber cycles.


 0 kommentar(er)
0 kommentar(er)
